Reading Configuration with Kleisli Arrows
In a previous article we looked at how Kleisli Arrows compose functions in a Monadic context.
A Kleisli Arrow is defined as follows:
Kleisli[F[_], A, B](run: A => F[B])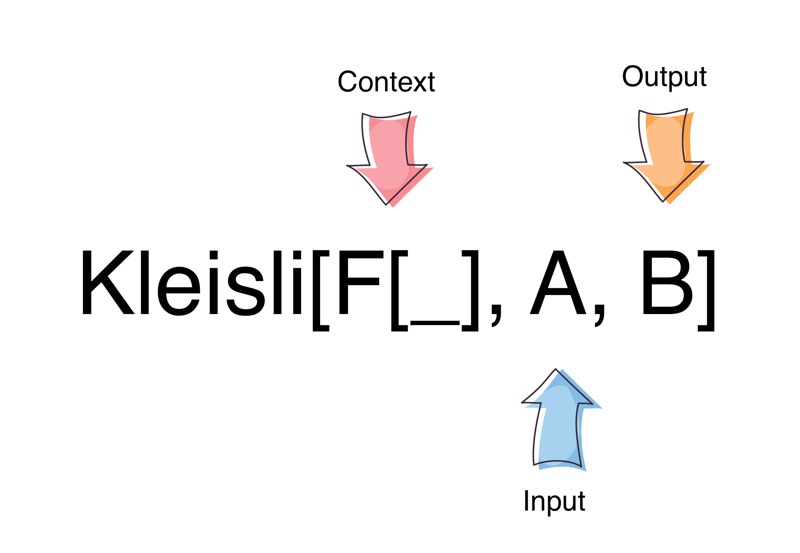
In essence it wraps a function:
A => F[B]Given some A, it returns a result B in a context F.
Reader and ReaderT
If we look at the signature of the Reader Monad, we see it wraps a somewhat similar function:
A => B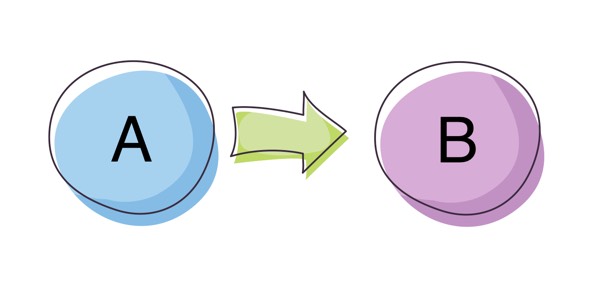
Given some A, it returns a B without any context.
A ReaderT Monad Transformer wraps the same function as that of a Kleisli Arrow:
ReaderT[F[_], A, B](A => F[B])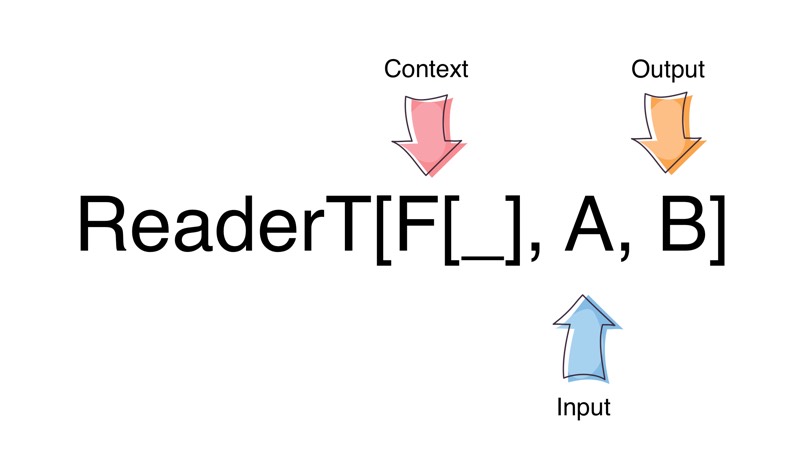
Given some A, it returns a B, in a context F.
A Kleisli Arrow has the same shape as (is isomorphic to) the ReaderT Monad. But what of its relationship to the Reader Monad?
An Id type constructor is a similar construct to the identity function, except that it returns the type supplied to it as opposed to the value:
type Id[A] = A // returns the type supplied
def identity[A](value: A): A = value //returns the value supplied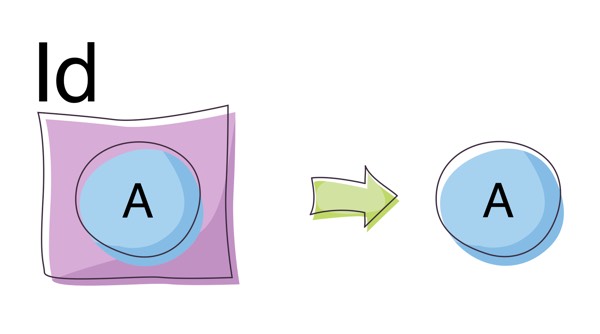
Armed with the Id type constructor we can define the Reader Monad in terms of the ReaderT Monad (and the Kleisli Arrow):
ReaderT[F[_], A, B] ==
ReaderT[Id, A, B] == //specialising for Id
ReaderT(A => Id[B]) ==
Reader(A => B) == //since Id[B] == B
Kleisli(A => B) //since ReaderT == KleisliIn Cats both the Reader and ReaderT Monads are defined in terms of a Kliesli Arrow:
type Reader[A, B] = Kleisli[Id, A, B]
type ReaderT[F[_], A, B] = Kleisli[F, A, B]Using Kleisli Arrows as a ReaderT
Lets try and use a Kleisli Arrow to read some configuration from the environment to yield something useful. In the following example we want to create a Person object from a Name and Age obtained from a Config object that holds both values:
final case class Name(first: String, last: String)
final case class Age(age: Int)
final case class Person(name: Name, age: Age)
final case class Config(name: String, age: Int)The creation of Name and Age have rules surrounding them and can fail if the rules are not met:
def readName: Config => Option[Name] = c => {
val parts = c.name.split(" ")
if (parts.length > 1) Option(Name(parts(0), parts.drop(1).mkString(" "))) else None
}
def readNameK = Kleisli(readName)
def readAge: Config => Option[Age] = c => {
val age = c.age
if (age >= 1 && age <= 150) Option(Age(age)) else None
}
def readAgeK = Kleisli(readAge)readNameK and readAgeK require a Config object to retrieve their values and are wrapped in a Kleisli Arrow. The Kleisli Arrow has to supply the same Config object to both functions. This is distinctly different to Kleisli composition where the output from one function was fed into the next. In this instance there is no composition between the two functions.
How would we go about combining these functions?
Since Kleisli Arrows map over functions in a Monadic context:
Kleisli[F[_], A, B] //F has a Monad instancewe can use a for-comprehension to solve our problem:
import cats.implicits._
val personK: Kleisli[Option, Config, Person] =
for {
name <- readNameK
age <- readAgeK
} yield Person(name, age)
//Some(Person(Name(Bojack,Horseman),Age(42)))
val result1 = personK(Config("Bojack Horseman", 42))
//None - Name is not space-separated
val result2 = personK(Config("Jake", 20))
//None - age is not between 1 and 150
val result3 = personK(Config("Fred Flintstone", 50000))Using Applicatives to Read Configuration
You might have noticed that the readAgeK function does not directly depend on the output of readNameK. This implies that we don’t have to use a Monad here (for-comprehesion) and can use something a little less powerful like Apply. The Apply typeclass is an Applicative without the pure function. The Kleisli data type has an instance for Apply with the following signature:
Apply[Kleisli[F, A, ?]]Let’s have a go at rewriting the Monadic code snippet with an Apply instead. We can use the ap2 function which has the following definition:
def ap2[A, B, Z](ff: F[(A, B) => Z])(fa: F[A], fb: F[B]): F[Z]Using ap2 we can create a Person instance as follows:
import cats.Apply
import cats.implicits._
type KOptionConfig[A] = Kleisli[Option, Config, A]
type PersonFunc = (Name, Age) => Person
val config = Config("mr peanutbutter", 30)
val readNameKOC: KOptionConfig[Name] = readNameK
val readAgeKOC: KOptionConfig[Age] = readAgeK
val personKOC: KOptionConfig[PersonFunc] = Kleisli( (_: Config) => Option(Person(_, _)))
//Kleisli[Option, Config, Person]
val personK = Apply[KOptionConfig].ap2(personKOC)(readNameKOC, readAgeKOC)
//Some(Person(Name(mr,peanutbutter),Age(30)))
personK(config)This solution while “less powerful” than the Monadic version, is somewhat uglier in Scala due to the type ascriptions on the individual functions.
We can also do something very similar using the map2 method:
def map2[A, B, Z](fa: F[A], fb: F[B])(f: (A, B) => Z): F[Z]which might be easier to reason about than ap2, but essentially they achieve the same result:
import cats.Apply
import cats.implicits._
type KOptionConfig[A] = Kleisli[Option, Config, A]
val config = Config("Diane Nguyen", 27)
val readNameKOC: KOptionConfig[Name] = readNameK
val readAgeKOC: KOptionConfig[Age] = readAgeK
//Kleisli[Option, Config, Person]
val personK = Apply[KOptionConfig].map2(readNameKOC, readAgeKOC) { Person(_, _) }
//Some(Person(Name(Diane,Nguyen),Age(27)))
personK(config)Kleisli Arrows with Different Inputs
One thing to note is that we keep aligning the input type, Config in this case, through all Kleisli Arrows.
How would we go about combining Kleisli Arrows with different input types?
This is where the local function comes into play. It is defined as:
def local[AA](f: AA => A): Kleisli[F, AA, B]
It basically converts a Kleisli[F, A, B] to a Kleisli[F, AA, B] as long as we supply it a function to convert an AA to A. The function f here converts some other input type AA into our required input type of A. This allows us to combine Kleisli Arrows with different input types as the local function, widens the input type to each Kleisli Arrow as AA.
Lets rewrite our previous example with Kleisli Arrows that take a String as input to readName and an Int as an input to readAge functions:
def readName: String => Option[Name] = name => {
val parts = name.split(" ")
if (parts.length > 1) Option(Name(parts(0), parts.drop(1).mkString(" "))) else None
}
def readAge: Int => Option[Age] = age => {
if (age >= 1 && age <= 150) Option(Age(age)) else None
}
def readNameK: Kleisli[Option, String, Name] = Kleisli(readName)
def readAgeK: Kleisli[Option, Int, Age] = Kleisli(readAge)We then widen the input types with the local function that takes a Config object:
import cats.implicits._
val personK: Kleisli[Option, Config, Person] =
for {
name <- readNameK.local[Config](_.name)
age <- readAgeK.local[Config](_.age)
} yield Person(name, age)
//Some(Person(Name(Bojack,Horseman),Age(42)))
personK(Config("Bojack Horseman", 42))
//None
personK(Config("Jake", 20))
//None
personK(Config("Fred Flintstone", 50000))And using map2 we get the same results:
import cats.Apply
import cats.implicits._
type KOptionConfig[A] = Kleisli[Option, Config, A]
val config = Config("Diane Nguyen", 27)
val readNameKOC: KOptionConfig[Name] = readNameK.local[Config](_.name)
val readAgeKOC: KOptionConfig[Age] = readAgeK.local[Config](_.age)
val personK = Apply[KOptionConfig].map2(readNameKOC, readAgeKOC) { Person(_, _) }
//Some(Person(Name(Diane,Nguyen),Age(27)))
personK(config)