Contravariant functors are Weird

Just a note about nomenclature before we start; I’ll use “functor” to represent the categorical meaning of the concept:

A functor is a mapping between categories

and Functor and Contravariant to specify the typeclass encodings of functors.

Let’s begin!

Contravariant functors are odd aren’t they? Covariant functors (which are modelled by the Functor typeclass) are quite straightforward but contravariant functors as their name implies seem to be the complete opposite.

Before we get into what a contravariant functor is, it’s useful to look at the Functor typeclass which we know and love.

Functor

A Functor is defined as:

class Functor f where
  fmap :: (a -> b) -> f a -> f b

We often understand a Functor to be a “container” or a “producer” of some type, where the function supplied to fmap is applied to the elements that are “contained” or “produced” in some type constructor¹ f.

A simple example would be the list ([]) type, that can represent zero or more values. Given a [a] we can turn it into a [b] when given a function a -> b.

data [] a = [] | a : [a]  -- an approximation of the [] data type

instance Functor [] where
  fmap _ [] = []
  fmap f (x:xs) = f x : fmap f xs

In the example below we convert a [Int] into a [String] given a function Int -> String:

import Data.Semigroup ((<>))

myInts :: [Int]
myInts = [1 .. 5]

emptyInts :: [Int]
emptyInts = []

intToString :: Int -> String
intToString n = (show n) <> "!"

myStrings :: [String]
myStrings = fmap intToString myInts -- ["1!","2!","3!","4!","5!"]

myEmptyString :: []
myEmptyString = fmap intToString emptyInts  -- []

Another example would the Maybe data type, that represents a value that may or may not exist.

data Maybe a = Nothing | Just a

instance Functor Maybe where
  fmap _ Nothing = Nothing
  fmap f (Just x) = Just (f x)

In the example below we convert a Maybe Int into a Maybe String given a function Int -> String:

import Data.Semigroup ((<>))

maybeInt :: Maybe Int
maybeInt = Just 10

notInt :: Maybe Int
notInt = Nothing

intToString :: Int -> String
intToString n = (show n) <> "!"

maybeString :: Maybe String
maybeString = fmap intToString maybeInt -- Just "10!"

notString :: Maybe String
notString = fmap intToString notInt -- Nothing

The Functor typeclass has laws, that ensure Functor instances behave in a predictable way.

Laws

Identity

fmap id == id

Essentially if you do nothing to the value of a Functor, you get the same Functor you started with.

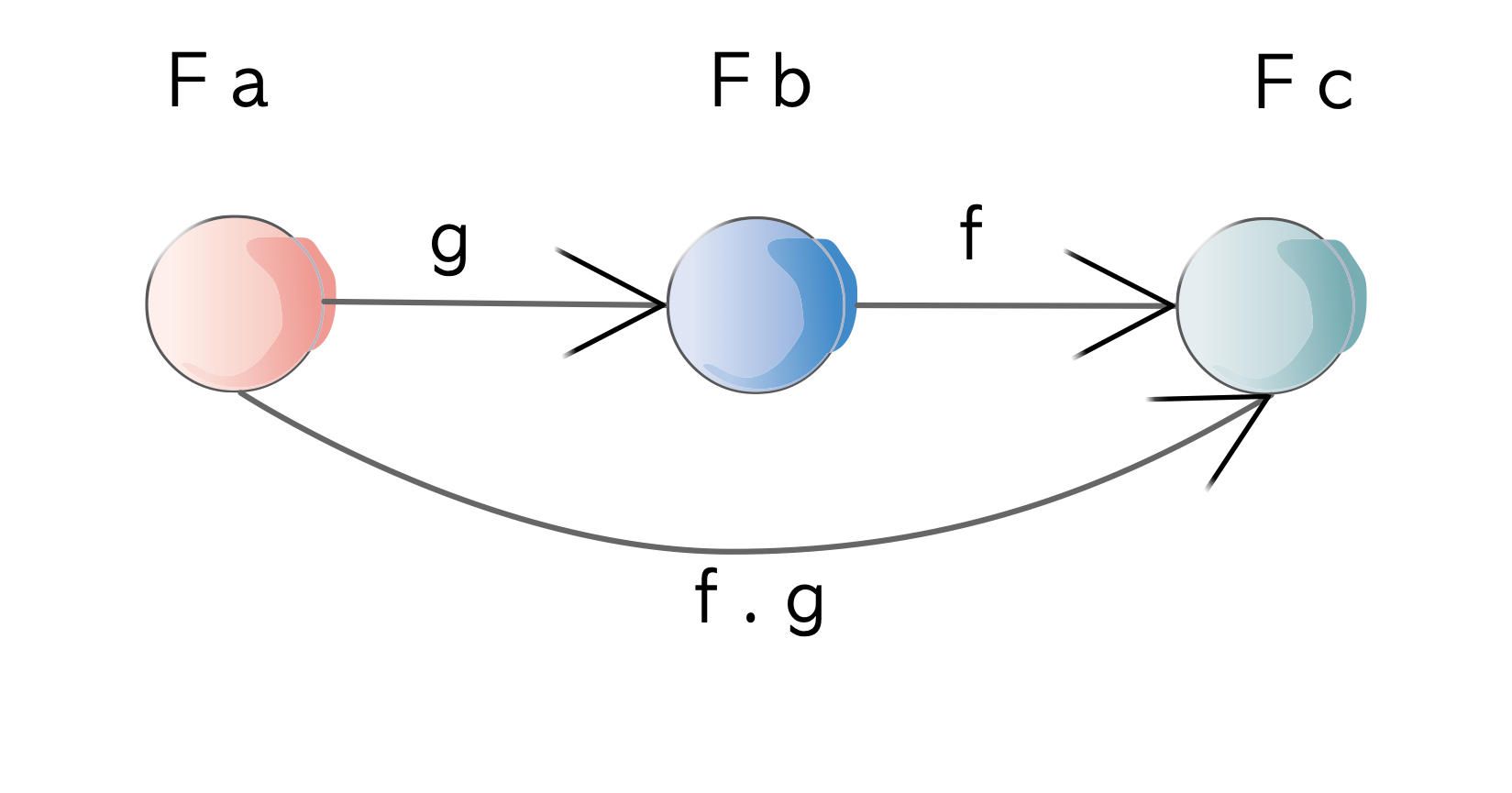
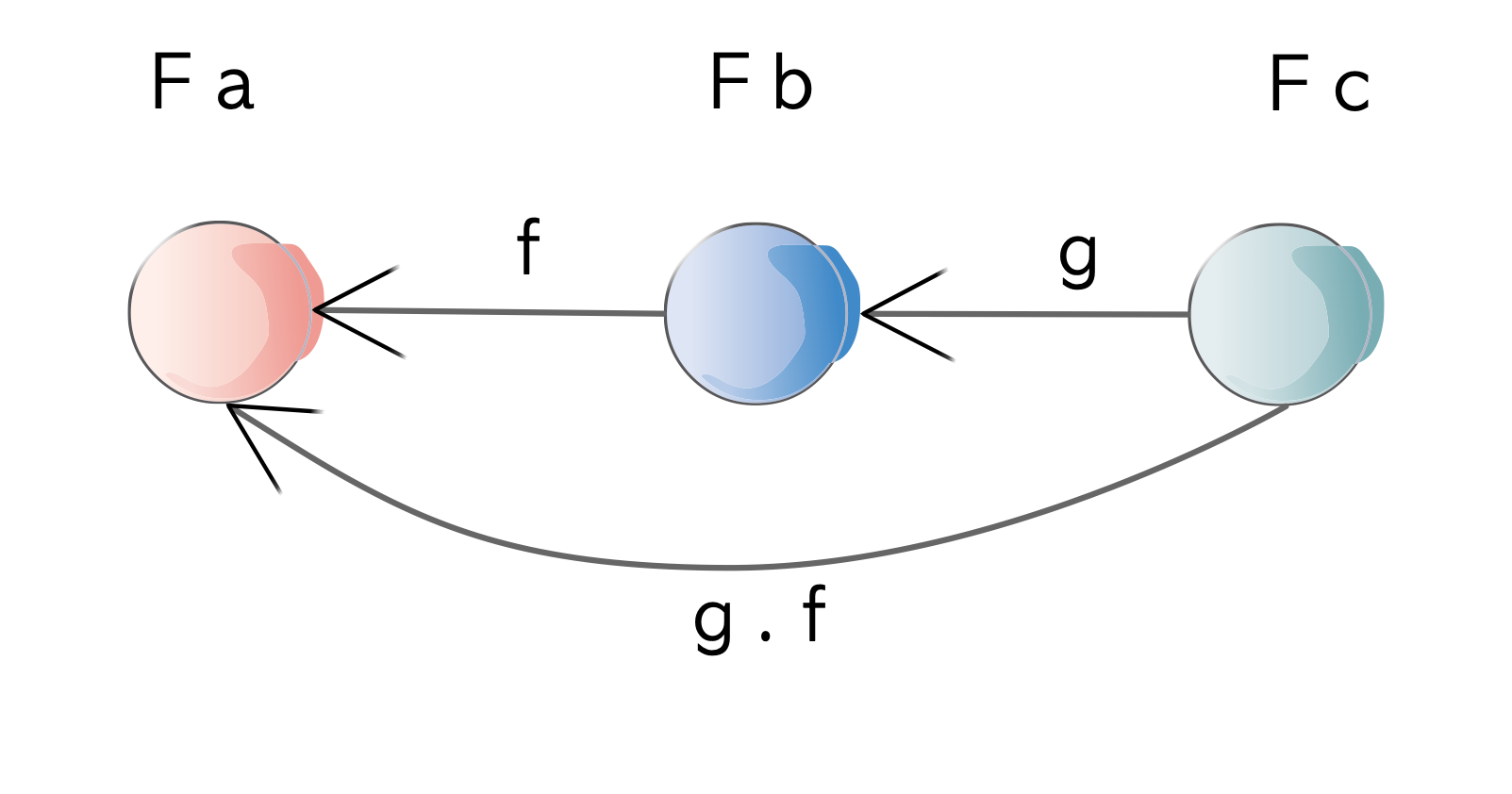
Composition

fmap (f . g) == fmap f . fmap g

If you convert the result of a Functor by fmaping with a function g and then fmaping that result with a subsequent function f, it’s the same as composing functions g and f (f . g) and then fmaping once.

The Wrong Type of fmap

Now let’s look at something a little different. Let’s create a data type to wrap a predicate of some sort. A predicate is something that will evaluate to a Bool:

newtype Predicate a = Predicate { getPredicate :: a -> Bool }

An example of a Predicate is greaterThanTen:

greaterThanTen :: Predicate Int
greaterThanTen = Predicate (\n -> n > 10)

that tests whether a number is greater than ten.

We can run with it getPredicate and an Int:

getPredicate greateThanTen 5  -- False
getPredicate greateThanTen 11 -- True

It could be useful to define a Functor instance for Predicate - say if we have a Predicate Int and we want to convert it into a Predicate String when we have a Int -> String function. Let’s try and implement that:

instance Functor Predicate where
  -- fmap (a -> b) -> Predicate a -> Predicate b
  fmap f (Predicate p) = Predicate (\b -> undefined)
  fmap f (Predicate (a -> Bool)) = Predicate (\b -> undefined)  -- expanding p
  fmap (a -> b) (Predicate (a -> Bool)) = Predicate (\b -> undefined) -- expanding f

Now we’ve run into a small problem:

How do we compose (a -> Bool) and (a -> b) to give us a (b -> Bool) ?

We are given a b but we don’t have access to any functions that actually use a b.

The problem is that we can’t. It’s because of something called “polarity” of the type variable a. No Functor instance for you Predicate.

Polarity

Polarity is a way of representing variance using the position of type variables. Let’s take a simple function a -> b as an example.

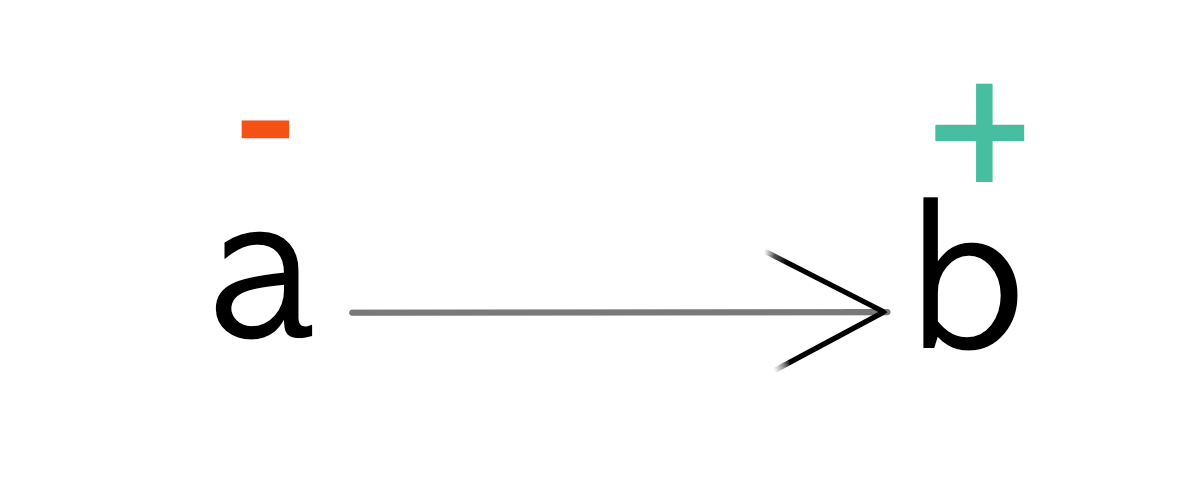
If a type variable is in input position like a it is given a negative polarity. If it is in an output position like b then it is given a positive polarity.

These polarities map directly to variant types.

Polarity	Variance
Positive	Covariant
Negative	Contravariant
Both	Invariant

What this means is that Functors (which are actually covariant functors) require a type constructor in a covariant position in order for you to define a Functor instance for that type.

Let’s look at a type that we know has a Functor instance like Maybe:

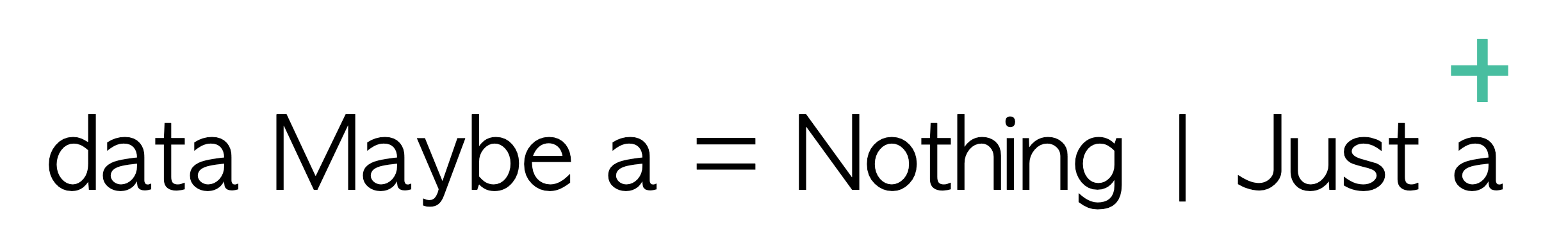
We can see that the type variable a occurs in a covariant (or output) position within the definition of the Just constructor.

Now let’s look at the definition of Predicate data type:

We can see that the type variable a occurs in a contravariant (or input) position. This indicates that we can’t create a (covariant) Functor instance for this data type.

But we want to map things! What do we do?

Contravariant

Welcome the Contravariant typeclass to the stage! It’s defined as:

class Contravariant f where
  contramap :: (a -> b) -> f b -> f a

Snazzy! Contravariant also takes some kind of type constructor f just like Functor but it has this weirdly named contramap function instead of fmap.

     fmap :: (a -> b) -> f a -> f b -- Functor
contramap :: (a -> b) -> f b -> f a -- Contravariant
                         ^^^

If we read fmap as:

If you have an a in some context and a function that takes that a and converts it to a b, I can give you a context with a b in it.

we can then read contramap as:

If you have a context that needs an a and a function that can convert bs to as, I can give you a context that needs bs.

But that probably doesn’t make much sense. So let’s try and look at this in terms of our non-Functor: Predicate. Predicate has a need for an a, which it then uses to tell if something about that a is True or False.

Let’s try and write a Contravariant instance for Predicate given that we know that the type a in Predicate occurs in an input position.

instance Contravariant Predicate where
  -- contramp (a -> b) -> f b -> f a
  contramap (a -> b) -> Predicate b -> Predicate a -- substituting for `f` for Predicate
  contramap aToB (Predicate bToBool) = Predicate (\a -> undefined)

Given that we have a function a -> b and essentially a function of type b -> Bool (wrapped inside a Predicate b), we can if given an a, convert it to a b using aToB and then give that b to bToBool to give us a Bool.

Here’s a slightly long-form implementation of the Contravariant instance for Predicate:

instance Contravariant Predicate where
  contramap :: (a -> b) -> Predicate b -> Predicate a
  contramap aToB (Predicate bToBool) =
    Predicate $ \a ->
      let b    = aToB a
          bool = bToBool b
      in bool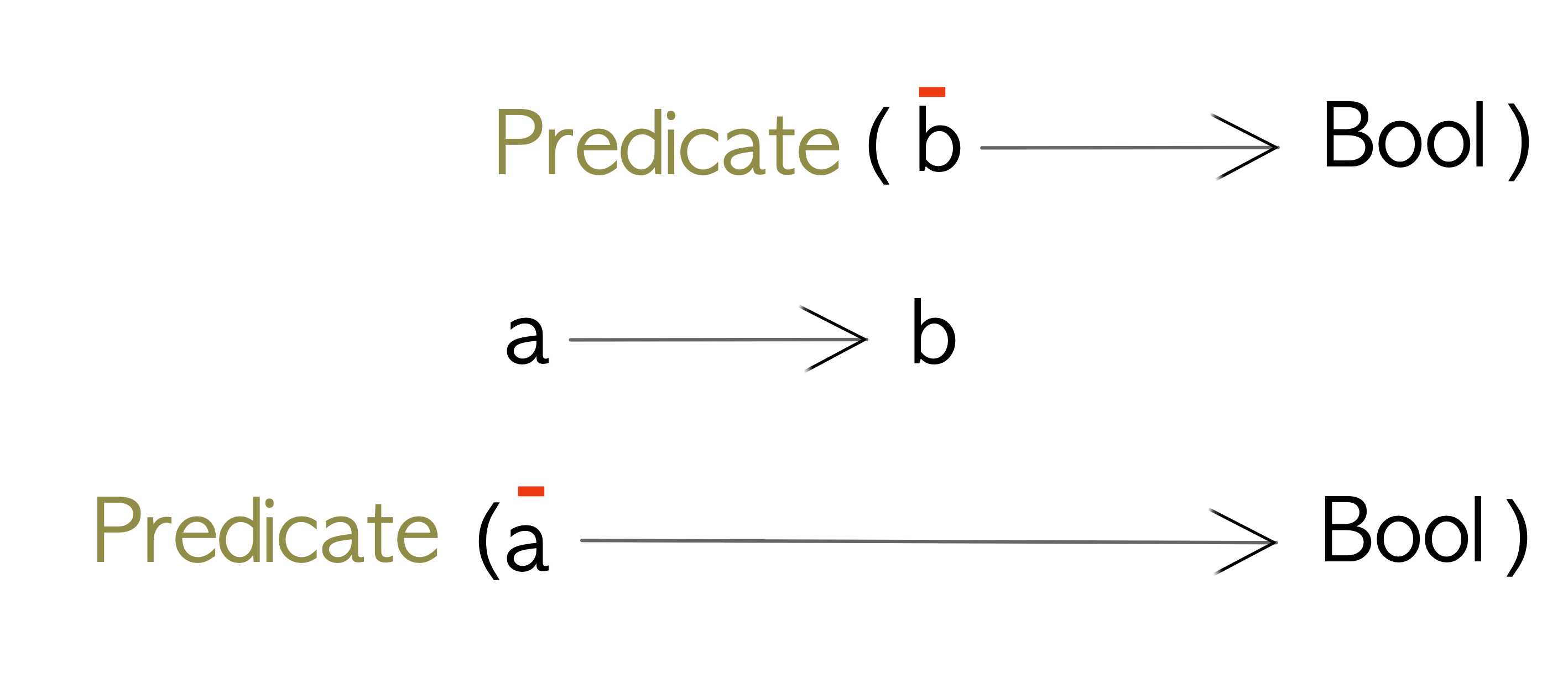

or more succinctly:

instance Contravariant Predicate where
  contramap :: (a -> b) -> Predicate b -> Predicate a
  contramap f (Predicate b) = Predicate $ b . f

We can see from the definition of Predicate a that all we are doing is running the supplied function f before the function within Predicate b. The reason we do that is to adapt a new input type to match an existing input type to gain some functionality.

If we revisit the (covariant) Functor instance for Maybe:

instance Functor Maybe where
  fmap _ Nothing = Nothing
  fmap aToB (Just a) = Just (aToB a)

we can see that the function aToB is run after we have a value of a. We do that to convert a result of some type to another type.

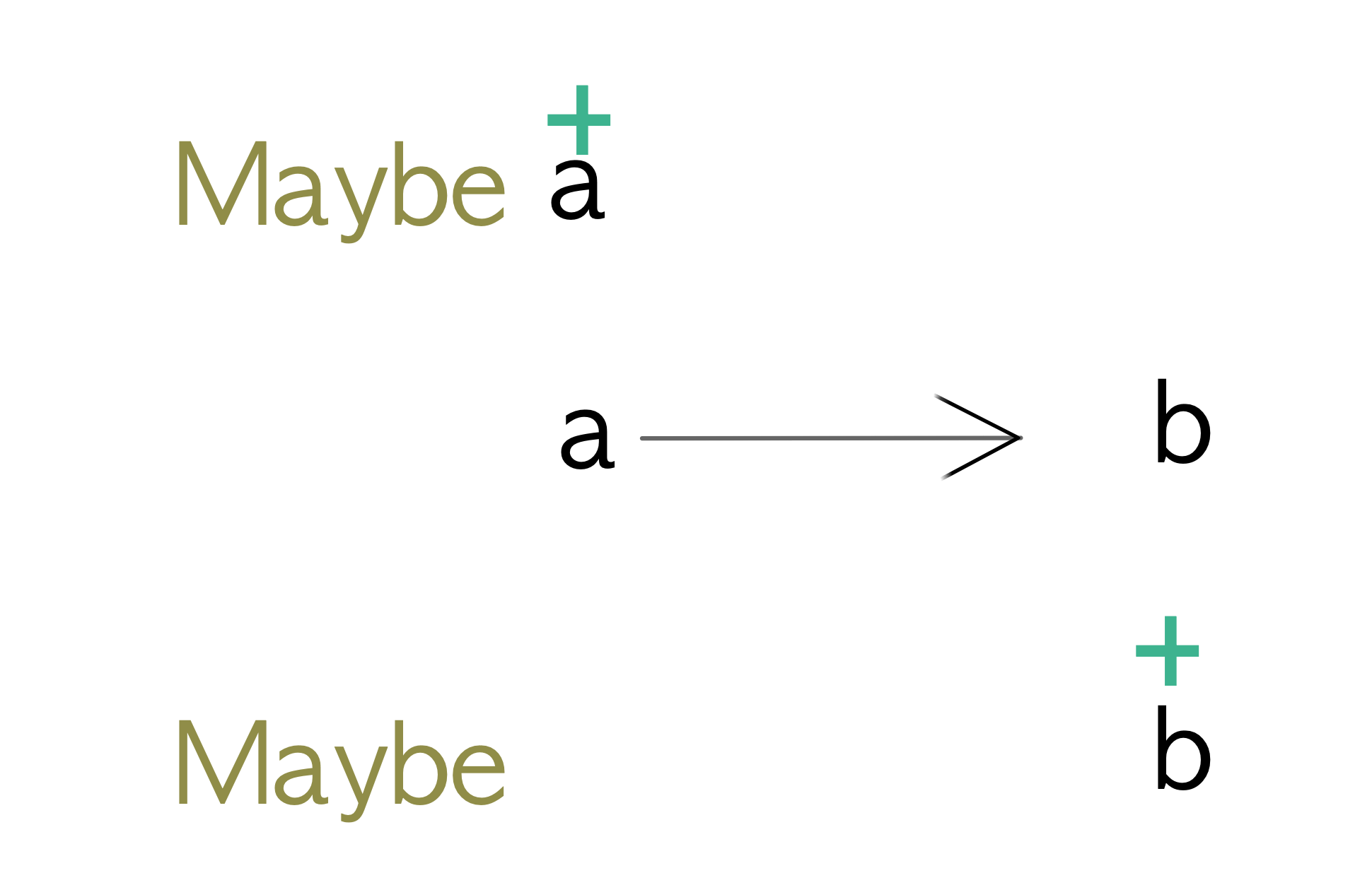
These are the essential differences between covariant and contravariant functors:

Typeclass	Function runs	Purpose
Functor	after	Convert results
Contravariant	before	Adapt inputs

Now that we know the essential difference between Functor and Contravariant, let’s look at how we can use contramap with our Predicate class.

Given that we already have a Predicate that determines whether a number is greater than ten:

numGreaterThanTen :: Predicate Int
numGreaterThanTen = Predicate (\n -> n > 10)

say we want to write another Predicate that verifies that the length of String is greater than ten characters.

strLengthGreaterThanTen :: Predicate String
strLengthGreaterThanTen = Predicate (\s -> (length s) > 10)

Sure, that’s pretty contrived but bear with me. Let’s also say we have a Person data type and we want to know if a person’s name is over ten characters long - if so we consider that to be a long name.

data Person = Person { personName :: String, personAge :: Int }

personLongName :: Predicate Person
personLongName = Predicate (\p -> (length . personName $ p) > 10)

And we can run these Predicates as:

getPredicate numGreaterThanTen 5 -- False
getPredicate numGreaterThanTen 20 -- True

getPredicate strLengthGreaterThanTen "hello"       -- False
getPredicate strLengthGreaterThanTen "hello world" -- True

getPredicate personLongName $ Person "John" 30        -- False
getPredicate personLongName $ Person "Bartholomew" 30 -- True

And this is fine, but there’s some duplication across each of the Predicates - namely the part where we compare a number to ten:

(\n -> n > 10)  -- Int
(\s -> (length s) > 10) -- String
(\p -> (length . personName $ p) > 10) -- Person

It would be nice if we didn’t have to repeat ourselves.

If we look at the differences between numGreaterThanTen, strLengthGreaterThanTen and personLongName we can see that the only difference is that one works on an Int and the others work on String and Person respectively. strLengthGreaterThanTen and personLongName each convert their input types to an Int and then do the same comparison:

Predicate (\(n :: Int) ->
  let num = id n
  in num > 10 -- (1)
) -- numGreaterThanTen


Predicate (\(s :: String) ->
  let num = length s
  in num > 10 -- (1)
) -- strLengthGreaterThanTen

Predicate (\(p :: Person) ->
  let name = personName p
      num  = length name
  in num > 10 -- (1)
) -- personLongName

The above expansion of the functions demonstrates that even though the Predicates themselves have different input types, at the end they are all converted to a number which is compared against the number ten. This is tagged with (1) in the above example.

We can also see that the only changes between the Predicates is the conversion from one type to another before running our comparison function (1). This is our clue that we can use contramap here to reuse some functionality.

numGreaterThanTen :: Predicate Int
numGreaterThanTen = Predicate (\n -> n > 10)

strLengthGreaterThanTen2 :: Predicate String
strLengthGreaterThanTen2 = contramap length numGreaterThanTen -- convert the String to an Int, then pass it to numGreaterThanTen

personLongName2 :: Predicate Person
personLongName2 = contramap (length . personName) numGreaterThanTen -- convert the Person to an Int, then pass it to numGreaterThanTen

We get the same results as before:

getPredicate strLengthGreaterThanTen2 "hello"       -- False
getPredicate strLengthGreaterThanTen2 "hello world" -- True

getPredicate personLongName2 $ Person "John" 30        -- False
getPredicate personLongName2 $ Person "Bartholomew" 30 -- True

Now we have rewritten strLengthGreaterThanTen and personLongName in terms of numGreaterThanTen by just running a function before it to convert the types. This is a simple example of a Contravariant Functor where we can reuse some existing functionality for a given type if we can convert from our other types to that type through some mapping function.

We can also go a little further and reuse even more:

personLongName3 :: Predicate Person
personLongName3 = contramap personName strLengthGreaterThanTen -- convert the Person to a String, then pass it to strLengthGreaterThanTen

Laws

Just like Functor has laws, Contravariant also has laws. This is awesome - because laws make our lives easier.

Identity

contramap id == id

Essentially if you do not change the value of a Contravariant functor, you get the same Contravariant functor you started with.

Composition

contramap f . contramap g = contramap (g . f)

If you convert the input to some Contravariant functor by contramaping with function g and then convert its input to some other type by contramaping again with a function f, it’s the same as composing the functions f and g (g . f) and then contramaping once. Notice the order of composition is switched as opposed to when we looked at the Functor laws.

Let’s take Predicate as an example and try out the identity law. The Contravariant instance for Predicate is defined as:

 instance Contravariant Predicate where
   contramap :: (a -> b) -> f b -> f a
   contramap f (Predicate p) = Predicate (p . f)

Given that we have a Predicate Int:

numGreaterThanTen :: Predicate Int
numGreaterThanTen = Predicate (\n -> n > 10)

Using contramap id on the above:

-- identity law
contramap id numGreaterThanTen == numGreaterThanTen

-- lhs
Predicate (p . f) -- applying contramap
Predicate (p . id) -- expanding f
Predicate (p) -- applying f
Predicate (\n -> n > 10) -- expanding p

-- rhs
numGreaterThanTen
Predicate (\n -> n > 10) -- expanding numGreaterThanTen

-- equality
lhs                      == rhs
Predicate (\n -> n > 10) == Predicate (\n -> n > 10)

Once again using Predicate as an example, let’s explore the compositional law of Contravariant.

Given that we have the following Predicates:

numGreaterThanTen :: Predicate Int
numGreaterThanTen = Predicate (\n -> n > 10)

length :: [a] -> Int
personName :: Person -> String

Using numGreaterThanTen, with length and personName:

-- composition law
contramap personName . contramap length $ numGreaterThanTen = contramap (length . personName) numGreaterThanTen


-- lhs
contramap personName . contramap length $ numGreaterThanTen
contramap personName . contramap length $ Predicate (\n -> n > 10) -- expanding numGreaterThanTen
contramap personName (Predicate $ \str ->
  let num  = length str
     bool  = num > 10
  in bool
) -- applying length
Predicate $ \person ->
  let str = personName person
      num = length str
     bool = num > 10
  in bool
) -- applying personName
=> Predicate Person

-- rhs
contramap (length . personName) numGreaterThanTen
contramap (\person ->
    let str = personName person
        num = length str
    in num
) numGreaterThanTen -- expanding length . personName
Predicate (\person ->
   let str  = personName person
       num  = length str
       bool = num > 10 -- expanding numGreaterThanTen
   in bool
)
=> Predicate Person

-- equality
lhs == rhs

Predicate (\person ->
  let str  = personName person
      num  = length str
      bool = num > 10
  in bool

) ==
Predicate (\person ->
   let str  = personName person
       num  = length str
       bool = num > 10
   in bool
)

Combinators

There are some built-in combinators that go with Contravariant.

Infix contramap

Similar to the contramap function the following functions can be used infix:

-- infixl 4
(>$<)        :: Contravariant f => (a -> b) -> f b -> f a
-- contramap :: Contravariant f => (a -> b) -> f b -> f a

A simple example of it in use:

p5 :: Predicate Int
p5 = Predicate $ \n -> n == 5

pLength5 :: Predicate [a]
pLength5 = length >$< p5

getPredicate pLength5 "hello"
-- True

getPredicate pLength5 "hello world"
-- False

Same as contramap but with the parameters switched:

-- infixl 4
(>$$<)       :: Contravariant f => f b      -> (a -> b) -> f a
-- contramap :: Contravariant f => (a -> b) -> f b      -> f a

Infix const

These combinators take in a constant input and completely ignore the input supplied when running the Contravariant instance.

-- infixl 4
(>$) :: b -> f b -> f a

It has a default implementation of:

(>$) :: b -> f b -> f a
(>$) = contramap . const

Let’s see how that works:

-- const when given two values returns the first value ignoring the second
const :: a -> b -> a
const x _ =  x

contramap :: Contravariant f => (a -> b) -> f b -> f a

(>$) :: b -> f b -> f a
(>$)      = contramap . const
(>$) b    = contramap (const b)   -- simplifying with b
(>$) b    = contramap (a -> b)    -- applying `const b`
(>$) b fb = contramap (a -> b) fb -- simplifying with fb
(>$) b fb = fa                    -- simplifying `contramap (a -> b) fb`

A simple example of it in use:

p5 :: Predicate Int
p5 = Predicate $ \n -> n == 5

pLength5 :: Predicate [a]
pLength5 = contramap length p5

getPredicate pLength5 "hello"
-- True

getPredicate pLength5 "hello world"
-- False

pAlwaysFalse :: Predicate [a]
pAlwaysFalse = 10 >$ p5

getPredicate pAlwaysFalse "hello"
-- False (because 10 /= 5)

getPredicate pAlwaysFalse "hello world"
-- False

Same as above but with the parameters switched:

-- infixl 4
($<) :: Contravariant f => f b -> b -> f a

LogAction

Let’s look at another example of Contravariant. Imagine you have the following data type that encapsulates performing some side effect on some polymorphic type a:

newtype LogAction a = LogAction { unlog :: a -> IO () }

For our purposes we can assume that we are going to use this to log some value either to the console or to a file or some other medium. This example has been adapted from the LogAction class of the CO-LOG logging library. Definitely check out the library for real-world uses of Contravariant and friends.

As we can see the type variable a occurs in input position so we should be able to define a Contravariant instance for it:

instance Contravariant LogAction where
  contramap :: (b -> a) -> LogAction a -> LogAction b
  contramap bToA logActionA = LogAction $ \b -> unlog logActionA (bToA b)

There should be no surprises here; we run the supplied function bToA on the input before passing it to the log action.

Here’s a slightly simplified implementation of the above:

instance Contravariant LogAction where
  contramap f logActionA = LogAction $ unlog logActionA . f

So how can we use LogAction? Let’s define a couple of implementations:

putStrLog :: LogAction String
putStrLog = LogAction putStr

putStrLnLog :: LogAction String
putStrLnLog = LogAction putStrLn

putStrLog and putStrLn are just wrappers around putStr and putStrLn from base. Both log a String to the console, the difference being that putStrLn sends a newline character to the console after each call.

Here’s how we’d use putStrLnLog:

unlog putStrLnLog "Hello World"
-- Hello World

Remember that LogAction needs an a which in this case is a String.

Now because we have the power of contravariance, we should be able to log out other types if we can convert them to a String.

Here are some examples:

-- simple function around contramap for LogAction
putStringlyLnLog :: (a -> String) -> LogAction a
putStringlyLnLog f = contramap f putStrLnLog

-- Now we can log Ints
putStrLnInt :: LogAction Int
putStrLnInt = putStringlyLnLog show

data Person = Person { name :: String, age :: Int }

-- custom String representation of Person
showPerson :: Person -> String
showPerson (Person name age) = "Person(name:" <> name <> ", age: " <> (show age) <> ")"

-- Now we can log people
putStrLnPerson :: LogAction Person
putStrLnPerson = putStringlyLnLog showPerson

-- custom String representation of Person that only displays age
showPersonAge :: Person -> String
showPersonAge person =  "age: " <> (show $ age person)

-- Additional Person LogAction which outputs only age
putStrLnPersonAge :: LogAction Person
putStrLnPersonAge = putStringlyLnLog showPersonAge

Here’s how we can run the above:

unlog putStrLnInt 42
-- 42

unlog putStrLnPerson $ Person "Neelix" 60
-- Person(name:Neelix, age: 60)

unlog putStrLnPersonAge $ Person "Tuvok" 240
-- age: 240

We can see that LogAction for Person, needs a Person instance as input to perform the log action.

Something that might not be obvious is that we can also adapt an input type to itself. It’s not necessary to always convert from one type to another.

Here are some example functions which we can use with contramap:

hello :: String -> String
hello = ("Hello" <>)

there :: String -> String
there = ("there" <>)

doctor :: String -> String
doctor = ("Doctor" <>)

space :: String -> String
space = (" " <>)

Here’s how we compose the above functions into a LogAction:

putStrLnGreeting :: LogAction String
putStrLnGreeting = contramap space . contramap doctor . contramap space . contramap there . contramap space . contramap hello $ putStrLnLog

Whoa! That’s even hard to read. What does it do? Remember from the second law of Contravariant that:

contramap f . contramap g = contramap (g . f)

Given that, we can rewrite our highly compositional LogAction like so:

putStrLnGreeting :: LogAction String
putStrLnGreeting = contramap  (hello . space . there . space . doctor . space) $ putStrLnLog

At least this is somewhat more readable - but the great thing is that knowing the laws helped us make our code more legible. But still - what does this do?

The trick is to remember that Contravaraint composition works in reverse to normal composition:

contramap f . contramap g = contramap (g . f) -- notice the (g . f) instead of (f. g)

This is how putStrLnGreeting is evaluated:

putStrLnGreeting :: LogAction String
putStrLnGreeting = contramap  (hello . space . there . space . doctor . space) $ putStrLnLog

unlog putStrLnGreeting "Switzer" -- run the logger with "Switzer" as the input

-- the input is going to go through this sequence of functions:
-- (hello . space . there . space . doctor . space)

-- applying space
" " <> Switzer
-- applying doctor
"Doctor" <> " " <> Switzer
-- applying space
" " <> "Doctor" <> " " <> Switzer
-- applying there
"there" <> " " <> "Doctor" <> " " <> Switzer
-- applying space
" " <> "there" <> " " <> "Doctor" <> " " <> Switzer
-- applying hello
"Hello" <> " " <> "there" <> " " <> "Doctor" <> " " <> Switzer
-- final output:
-- Hello there Doctor Switzer

Let’s look at one more LogAction which might be interesting; One where we ignore the input and return some constant output:

override :: a -> a -> a
override value = const value

A we mentioned previously, const is defined as a -> b -> a, where it accepts two inputs but returns the value of the first input (ignoring the second input).

Here’s how we use it with LogAction:

qPutStrLn ::LogAction String
qPutStrLn = contramap (override "This is Q!!") putStrLnLog

-- run it
unlog qPutStrLn "Picard J L"
-- This is Q!!

Now if our memory serves, we should be able to do the same with >$:

qPutStrLnOp :: LogAction String
qPutStrLnOp = "This is Q!!" >$ putStrLnLog

-- run it
unlog qPutStrLnOp "Sisko B L"
-- This is Q!!

Equality and Ordering

Now let’s look at two somewhat related concepts: equality and ordering

Equivalence

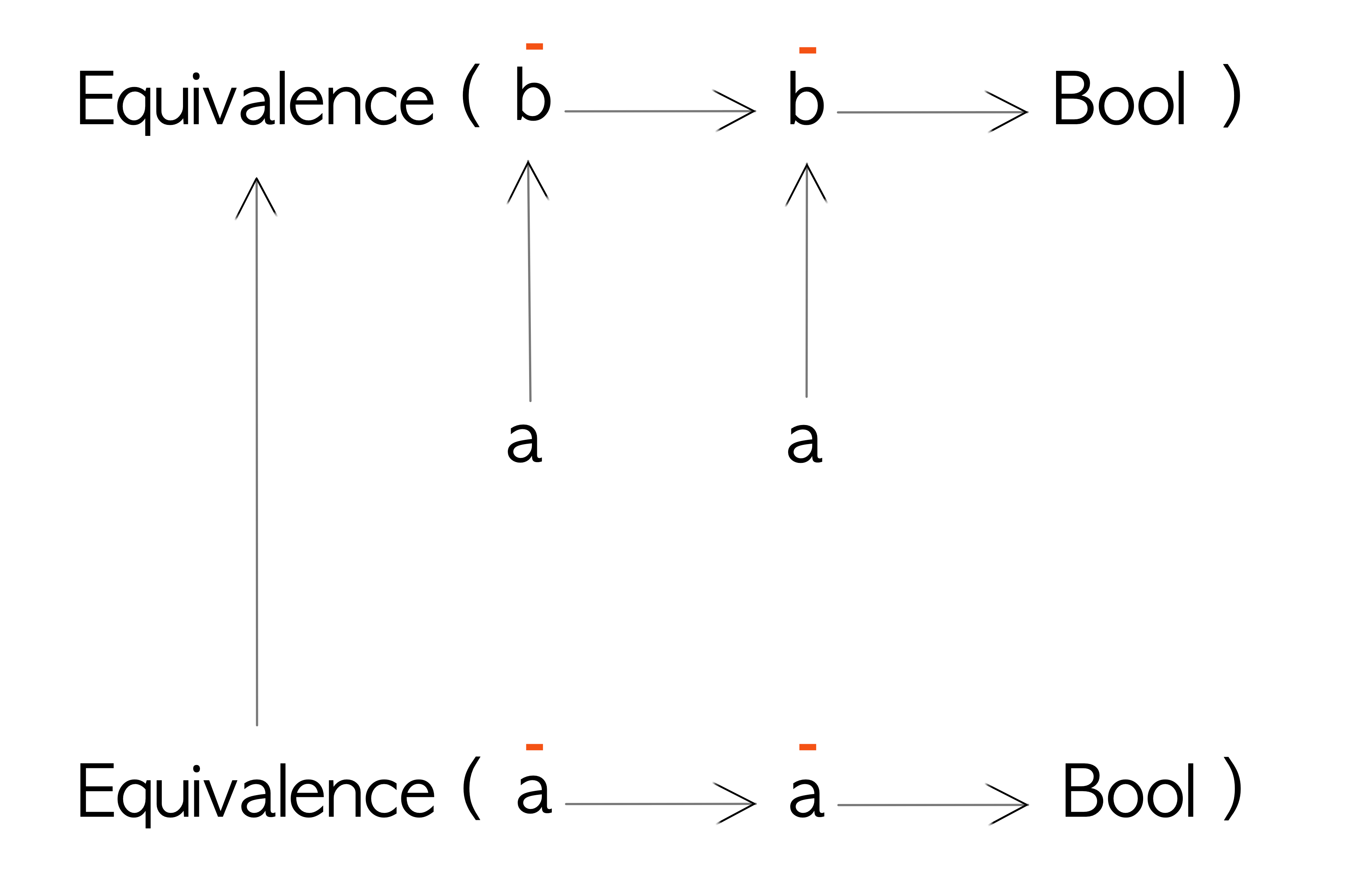
Let’s imagine that we have a datatype called Equivalence that wraps an equality expression:

newtype Equivalence a = Equivalence { getEquivalence :: a -> a -> Bool }

Given two values of type a the getEquivalence function will return a Bool indicating if they are equal or not.

Now we can see that both a type variables are in input position. Let’s define a Contravariant instance for it:

instance Contravariant Equivalence where
  contramap :: (a -> b) -> Equivalence b -> Equivalence a
  contramap aToB (Equivalence eqB1B2) = Equivalence $ \a1 a2 ->
    let b1 = aToB a1
        b2 = aToB a2
    in eqB1B2 b1 b2

Something important to note is that the function we supply to contramap (a -> b) is run on twice - once on each of the input parameters (b).

Given an Equivalence for Int:

intEq :: Equivalence Int
intEq = Equivalence (==)

We can run it as:

getEquivalence intEq 1 2
-- False

getEquivalence intEq 1 1
-- True

We can calculate the equivalence of other types using contramap:

strLengthEq :: Equivalence String
strLengthEq = contramap length intEq

data Person = Person { name :: String, age :: Int }

personAgeEq :: Equivalence Person -- equality by age
personAgeEq = contramap age intEq

personNameLengthEq :: Equivalence Person -- equality by length of name
personNameLengthEq = contramap name strLengthEq

Here’s how we can run the above:

-- t1 = Person "Tuvok1" 240
-- t2 = Person "Tuvok2" 340
-- t3 = Person "Neelix" 60
-- t4 = Person "Janeway" 40

getEquivalence personAgeEq t1 t2
-- False

getEquivalence personAgeEq t1 t1
-- True

getEquivalence personAgeEq t2 t2
-- True

getEquivalence personAgeEq t2 t3
-- False

getEquivalence personNameLengthEq t1 t2
-- True

getEquivalence personNameLengthEq t3 t4
-- False

getEquivalence personNameLengthEq t1 t4
-- False

Comparison

Let’s imagine that we have a datatype called Comparison that wraps a comparison expression:

newtype Comparison a = Comparison { getComparison :: a -> a -> Ordering }

Given two values of type a the getComparison function will return an Ordering (LT, GT or EQ) with respect to each other.

Now we can see that both a type variables are in input position as before. Let’s define a Contravariant instance for it:

instance Contravariant Comparison where
  contramap :: (a -> b) -> Comparison b -> Comparison a
  contramap aToB (Comparison cmpB1B2) = Comparison $ \a1 a2 ->
    let b1 = aToB a1
        b2 = aToB a2
    in cmpB1B2 b1 b2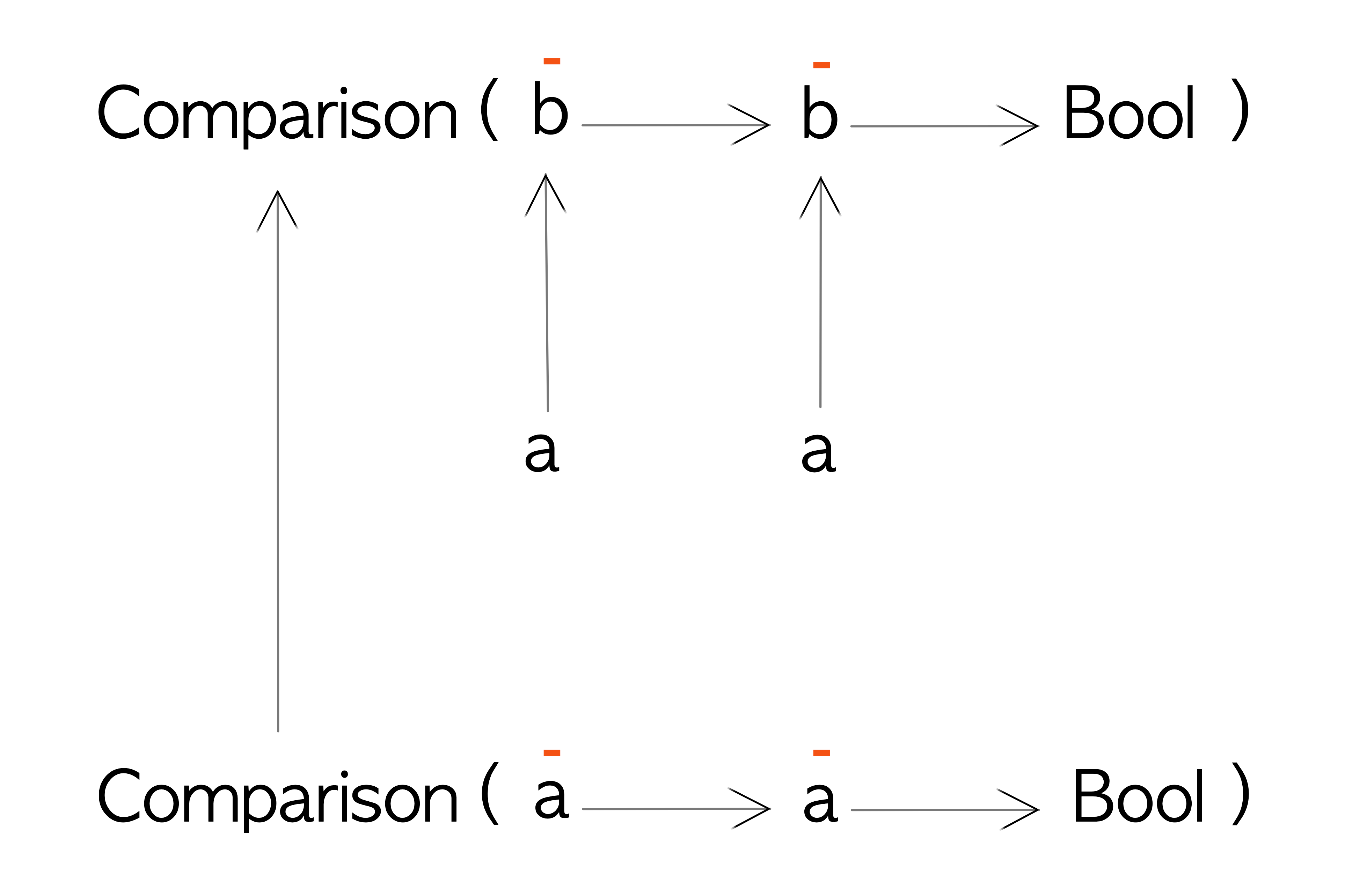

We can see that the wrappers for Equivalence and Comparison are almost the same, as are their Contravariant instances.

Given a Comparison for Int as:

intCmp :: Comparison Int
intCmp = Comparison compare

We can run it as:

getComparison intCmp 1 1
-- EQ

getComparison intCmp 1 2
-- LT

getComparison intCmp 2 1
-- GT

We can now calculate the comparison of other types using contramap:

strCmp :: Comparison String
strCmp = contramap length intCmp

personAgeCmp :: Comparison Person
personAgeCmp = contramap age intCmp

fstCmp :: Comparison a -> Comparison (a, b)
fstCmp compA = contramap fst compA

Nothing new here. Let’s have a look at how to sort numbers. We use the sortBy function defined in Data.List from the base package:

sortBy :: (a -> a -> Ordering) -> [a] -> [a]

We can see from the sortBy function definition that it can accept the data wrapped in the Comparison data type:

sortBy        :: (a -> a -> Ordering) -> [a] -> [a]
getComparison ::  a -> a -> Ordering

Sorting numbers with the above function:

-- unsortedNumbers = [3, 5, 1, 4, 2]

-- ascending sort
sortBy (getComparison intCmp) unsortedNumbers
-- [1,2,3,4,5]

-- descending sort
sortBy (flip $ getComparison intCmp) unsortedNumbers
-- [5,4,3,2,1]

Notice how we just use the flip function to change between ascending and descending sort:

flip :: (a -> b -> c) -> b -> a -> c

flip just changes the order of input parameters. flip is awesome :) I saw this technique first used at Roman Cheplyaka’s blog.

But here’s something interesting: since we know how to sort Ints we also know how to sort people by age via personAgeCmp! Let’s see that in action:

-- unsortedPeople = [Person "Tuvok1" 240, Person "Janeway" 40, Person "Neelix" 60]

-- ascending sort
sortBy (getComparison personAgeCmp) unsortedPeople
-- [Person {name = "Janeway", age = 40},Person {name = "Neelix", age = 60},Person {name = "Tuvok1", age = 240}]

-- descending sort
sortBy (flip $ getComparison personAgeCmp)
-- [Person {name = "Tuvok1", age = 240},Person {name = "Neelix", age = 60},Person {name = "Janeway", age = 40}]

Function Types

A regular function can be though of being defined as:

newtype RegularFunc a b = RegularFunc { getRegular :: a -> b }

We can define a Functor instance for RegularFunc because b is in output position. But what about a, which is in input position? More on that below.

Let’s recall what the definition of the Functor type class looks like:

class Functor f where
  fmap :: (a -> b) -> f a -> f b

In the above declaration, f is a type constructor with one type hole. Given RegularFunc which has two type holes (a and b), we need to fill one in, in order to use it with the Functor instance implementation. To do this we fix a and get the type constructor RegularFunc a. We can’t fix b as partial application of types is done from left to right (holes can only be on the right).

instance Functor (RegularFunc a) where
  fmap :: (b -> c) -> f b -> f c
  fmap = (.)

We can’t define a Contravariant instance for a because we have to fix a (we can’t define behaviour over it). All we have to play with is b which is in output position (and hence covariant)

Oh! Come on! If only we didn’t have to fix a. What if we could fix b instead? We don’t care about b. b is dead to us.

Let’s dream up such a type and call it Op - for opposite of regular:

newtype Op a b = Op { getOp :: b -> a }

Now we can see that the type b is in input position within the data type. It’s also on the right of Op a b which means we don’t have to fix it.

Op a b can be a little confusing because we have switched the position of type parameters a and b as they were in RegularFunc; a is the output and b is the input.

Data type	Polarity of a	Polarity of b
RegularFunc a b	Input	Output
Op a b	Output	Input

And guess what? We can now fix a (which is now our output) and can define a Contravariant instance for Op:

instance Contravariant (Op a) where
  contramap :: (c -> b) -> Op a b -> Op a c
  contramap cToB (Op bToA) = Op $ \c ->
    let b = cToB c
    in bToA b

Here’s a simple example of how to use it:

stringsLength :: Op Int [String]
stringsLength = Op $ sum . fmap length

unqiueStringsLength :: Op Int (S.Set String)
unqiueStringsLength = contramap S.toList stringsLength

If we know how to sum all the lengths of a [String] we can adapt that function to sum the lengths of a Set of String:

import Data.Set (fromList)

namesList = ["Paris", "Kim", "B'Elanna", "Seven"]
namesSet  = fromList namesList

getOp stringsLength $ namesList
-- 21

getOp unqiueStringsLength $ namesSet
-- 21

Now Predicate, Comparison, Equivalence and Op seem like useful data structures. The good news is that they already exist in the Data.Functor.Contravariant package from base so you don’t have to write them yourself.

One interesting implementation detail of the Comparison and Equivalence Contravariant instances is that they are implemented using the on function:

newtype Equivalence a = Equivalence { getEquivalence :: a -> a -> Bool }

instance Contravariant Equivalence where
  contramap f g = Equivalence $ on (getEquivalence g) f

The on function is defined as:

on :: (b -> b -> c) -> (a -> b) -> a -> a -> c
(.*.) `on` f = \x y -> f x .*. f y

Essentially given a function b -> b -> c and a function a -> b, the second function will be applied to each input of type a converting it to a b and then the first function is applied on the transformed inputs. Such reuse. :)

More Polarity

Let’s take a look at the CallbackRunner example from FP Complete:

newtype CallbackRunner a =
  CallbackRunner {
    runCallback :: (a -> IO ()) -> IO ()
  }

Type variable a is in input position so we should be able to write a Contravariant instance for it:

instance Contravariant CallbackRunner where
  contramap :: (a -> b) -> CallbackRunner b -> CallbackRunner a
  contramap aToB (CallbackRunner runCallbackB) = CallbackRunner $ \aToIO ->
    runCallbackB $ \b ->
      let a = undefined -- where do we get an `a` from?
      in aToIO a

-- if we had a (b -> a) we could convert the `b` to an `a`

Hmm. Now it looks like we have a problem. There doesn’t seem to anyway for us to get an a to pass to aToIO to complete the implementation. We have a b and if there was a function b -> a instead of our a -> b, we could convert that b to an a and it would all work.

This is because there’s more to the polarity story than I’ve shared up until now. While a is in input position in a -> IO(), it’s polarity changes when it’s also used as an input to the function (a -> IO ()) -> IO (). I previously mentioned that an input position is a negative polarity and an output position is a positive polarity.

To figure out the final polarity of something we need to multiply its polarities at every context it is used within in the function definition. More on this below.

Polarity multiplication is similar to the multiplication of positive and negative numbers:

Polarity Multiplication Table

Polarity1	x	Polarity2	Polarity
Positive	x	Positive	Positive
Positive	x	Negative	Negative
Negative	x	Positive	Negative
Negative	x	Negative	Positive

Let’s try and figure out the polarity of a given our new found multiplication skills. Given runCallback:

runCallback :: (a -> IO ()) -> IO ()

a is in input or negative position in:

a -> IO ()

but within whole function it’s a slightly different story:

(a -> IO ()) -> IO () -- func
x = (a -> IO ())      -- assigning (a -> IO ()) to x in func
x -> IO ()            -- substituting x in func

We can see that x in the above example is in input or negative position as well. Given that x is a -> IO ():

(a -> IO ()) -> IO ()
-- a -> IO (a is negative)
-- (a -> IO ()) -> IO () (the whole parenthesis are in negative position)
-- polarity of a: negative * negative = positive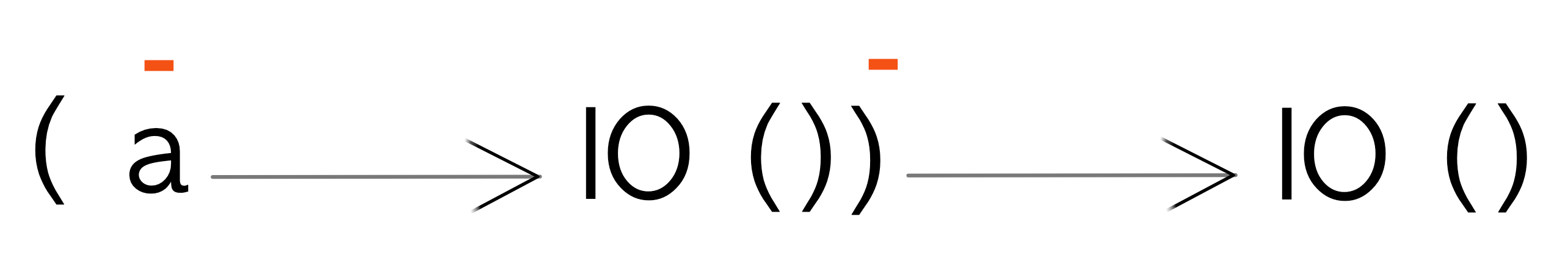

Given that a is now in output or positive position, we should be able to write a Functor instance for it:

instance Functor CallbackRunner where
  fmap :: (a -> b) -> CallbackRunner a -> CallbackRunner b
  fmap aToB (CallbackRunner runCallbackA) = CallbackRunner $ \bToIO ->
    runCallbackA $ \a ->
      let b      = aToB a
          result = bToIO b
      in result

And we can!! If you want to dig more into polarities there are some good exercises at the FP Complete article.

Invariant Functors

We briefly mentioned invariant functors when talking about Polarity but never mentioned them again until now. The Invariant typeclass is the parent typeclass of both Functor and Contravariant)

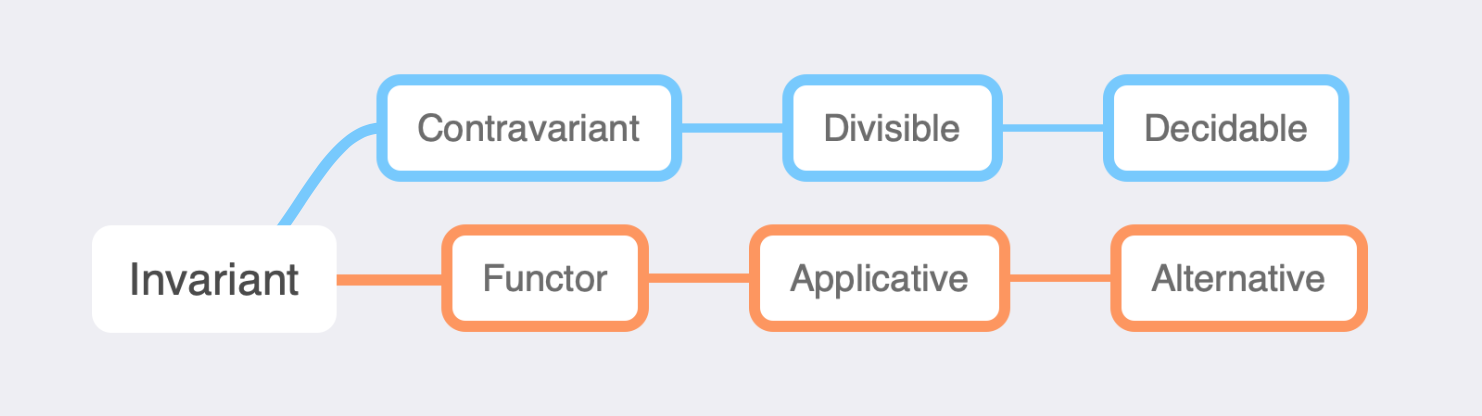
Given that this post is quite long, I’m only going to mention that Invariant has both covariant and contravariant functions in its definition:

class Invariant f where
  invmap :: (a -> b) -> (b -> a) -> f a -> f b

where a -> b is the function to use if f a is a Functor and b -> a is the function to use if f a is Contravariant.

I may write another article about invariant functors if I feel the need for it, but in the meantime checkout these articles to get you started.

Summary

Hopefully this has shed some light onto contravariant functors and how they are used and how they can be implemented. In a future article I hope to cover Divisible and Decidable typeclasses that build up from Contravariant.

The source for this article can be found on Github.

A big “Thank You” to George Wilson for inspiring me to dig deeper into this topic with his excellent presentations on Functors.

A big thanks also to Andrew Newman who reviewed this article.

Epilogue

Just when you thought you’d learned all there is to learn about variance, there appears to be a variance of the fourth kind. It’s known as phantom variance or bivariance as pointed by emilypii and dbramucci on reddit. dbramucci also linked to a nice Scala slidedeck from Michael Pilquist

Definitions

Type constructor (1)

A data type that needs one or more type variables to be fully defined.

For example, Maybe is a type constructor and Maybe Int is a type.

Contravariant functors are Weird

Functor

Laws

Identity

Composition

The Wrong Type of fmap

Polarity

Contravariant

Laws

Identity

Composition

Combinators

Infix contramap

Infix const

LogAction

Equality and Ordering

Equivalence

Comparison

Function Types

More Polarity

Polarity Multiplication Table

Invariant Functors

Summary

Epilogue

Links

Articles

Video

Books

Questions and Answers

Packages

Definitions

Type constructor (1)